Density Functional Theory (DFT) is the most used electronic-structure computational method in quantum chemistry and condensed matter physics, since it provides the highest accuracy/computational cost ratio. In combination with powerful High-Performance Computing (HPC) hardware resources, DFT allows first principles calculations of the electronic and optical properties of systems with thousands of atoms.
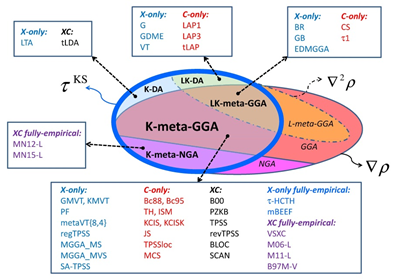
However, despite DFT is exact in principle, its practical accuracy depends on approximations concerning the exchange-correlation (XC) energy as a functional of the ground-state electronic density. In case of orbitalfree or subsystem-DFT calculations, approximations of the non-interacting kinetic energy (KE) functional are also required.